The story of Reversi42 began many years ago, in an age when the word “smart working” didn’t even exist. Every morning, far more carefree than I am today, I would take the subway to work with a tiny 10-inch netbook. In that cramped space, I started developing the first version of my Reversi42 engine – supported by a colleague who was an expert Othello player.

I wanted to see how far I could go with minimal hardware and a few weeks of focus.
I coded offline, using my first version of Python and my beloved Vim, inside a GNU/Linux terminal where every pixel truly mattered.
The first stable release came on March 7, 2011.
VISIT THE OLD ARTICLE ABOUT REVERSI42
Years later, I reopened that old GitHub repository because I wanted to transform a legacy project into a modern testbed. I wanted to see what would happen when a prehistoric project, written in 2011 on a subway using Vim and a netbook, met the tools of 2025.
And I asked myself: how much can I build today in just a few days – backed by years of experience and the best AIs around?
Spoiler: much more than I could ever have imagined and my expectations were already high.
That’s how I opened a temporal rift, short-circuiting past and present – between the magical Vim formulas that once carried me to nirvana and the modern oracle of Cursor.
Disassemble. Rebuild. Amplify.
The new Reversi42 distills everything I’ve learned over the years:
- SOLID design principles
- Clear responsibilities, modular architecture
- Heavy use of design patterns
- A more rational, readable, testable engine
- Iterative deepening and refined alpha-beta pruning
- Clean heuristics and early transposition table optimizations
- Modern responsive UI with WebSockets
- A CI/CD pipeline
It felt like having a conversation with a younger version of myself – same passion, entirely new tools.
How Cursor Changed the Game
Cursor empowered me to:
- Perform deep structural refactoring
- Anticipate and analyze edge cases in move logic
- Compress the think-code-verify cycle
- Clarify architectures, patterns, and responsibilities
It didn’t write the code for me but it amplified my thinking, accelerating productivity to vertiginous levels. I spent nights coding without realizing time was passing.
Working with Cursor introduced me to a new programming paradigm.
Yet such power demands discipline, with experience, you learn how to guide it instead of being guided by it.

The New Reversi42
- Modern Web UI – Browser-based interface with real-time WebSocket updates
- Ultra-Fast Bitboard Engine – 50-100× faster than standard implementations
- AI Gladiators – Distinct opponents from beginner to champion, each with unique play styles and Midjourney-generated avatars
- No-Code AI Creation – Configure AI players via YAML (zero programming!)
- New AI Engine “Apocalyptron” – Super-modular and high-performance
- Opening Book System – Professional opening sequences
- Tournament Mode – Run AI competitions and benchmarks
- Highly Configurable – 200+ parameters per AI, 4 evaluation presets, parallel search
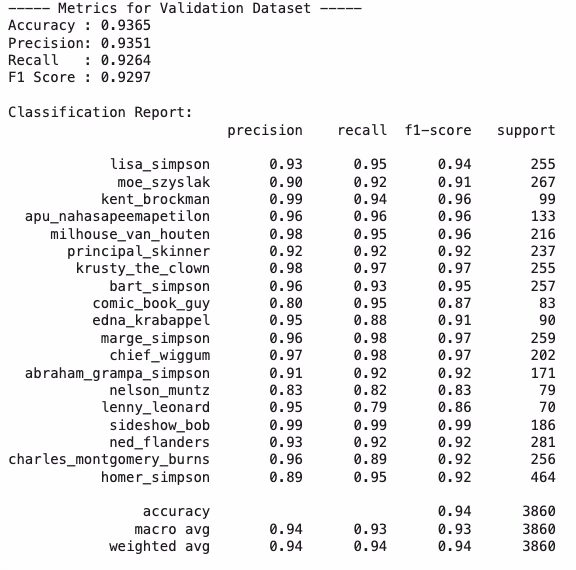
- Extensive Testbook – ~220 tests on the AI engine and 410 across the rest of the codebase
…and much more.
Here are the available AI players:
 | DIVZERO.EXE The singularity has arrived | Ultimate AI entity with adaptive depth. Cold, calculating, and merciless – the embodiment of strategic perfection. |
 | The Oracle Prophetic vision activated | Mystical seer specializing in endgame prophecy, seeing 14 moves ahead. Unstoppable in the endgame. |
 | Fortress Eternal The fortress stands eternal | Impenetrable defensive master building walls of stability. The immovable object. |
 | The Executioner Judgement has been passed | Ruthless destroyer seeking tactical annihilation. Merciless aggression hunting for kill shots. |
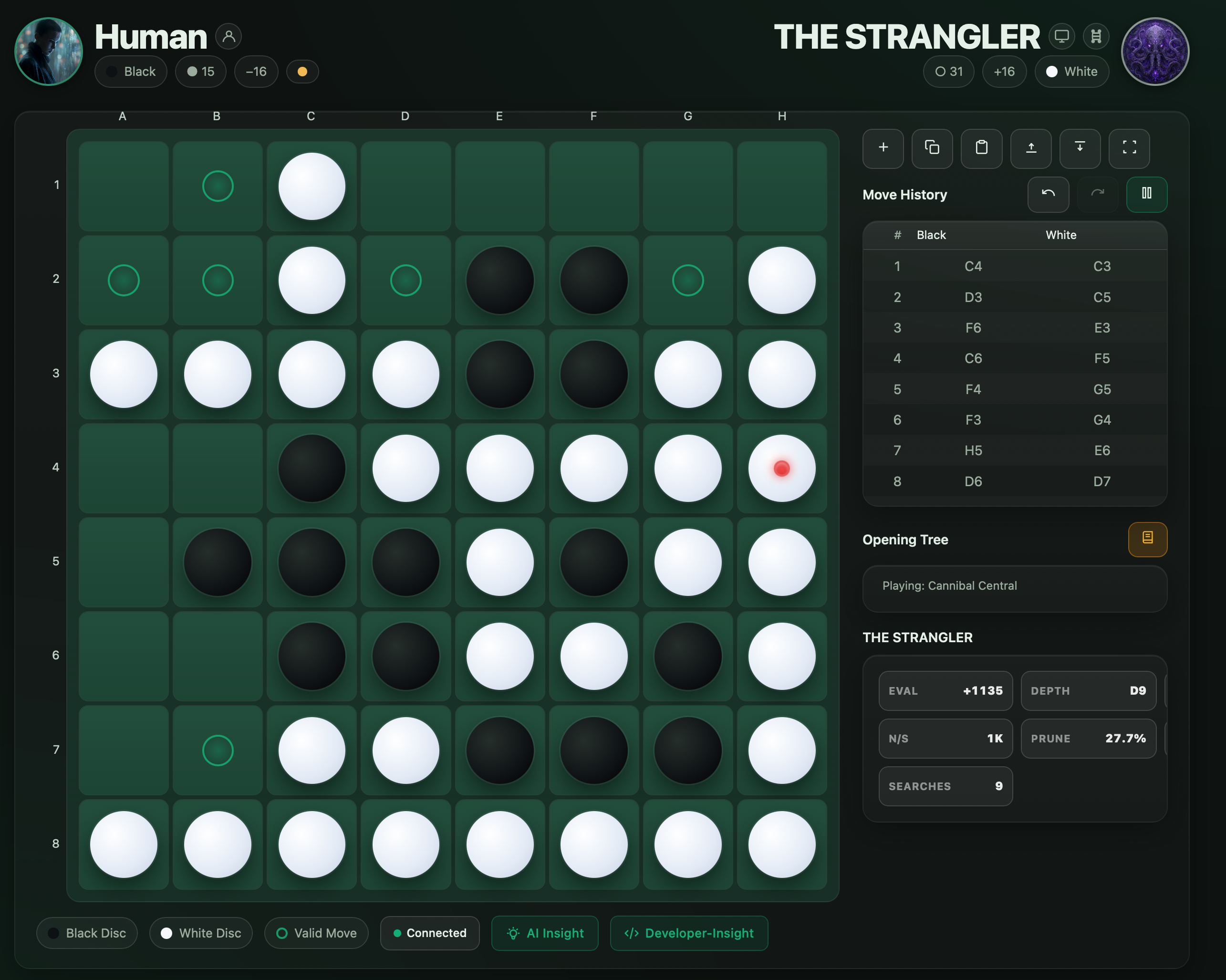
 | The Strangler Feel your options disappear | Mobility assassin suffocating opponents by eliminating their options. Creates zugzwang positions. |
 | Corner Reaper The corners belongs to me | Obsessive corner specialist treating corners as sacred territory. Corners are permanence, and permanence is victory. |
 | Lightning Strike Speed mode activated | Blitz master valuing speed above all. Makes decisions in milliseconds. Sometimes the fastest move is the best move. |
 | Glitch Lord Reality.exe has stopped working | Chaotic anomaly embracing unpredictability. Controlled randomness makes it impossible to predict. |
 | Blitz Demon Blink and yu’ll miss it | Speed incarnate, faster than thought. Moves in under 50 milliseconds. Being first is more important than being best. |
 | Zen Master Find balance in all things | Enlightened teacher embodying perfect balance. Patient and educational-seeks to teach, not destroy. |
 | Apocalyptron The Apocalypse Engine | Ultimate configurable engine – a platform of infinite possibilities. True power comes from flexibility. |
🚀 🚀 VISIT THE DEDICATED REVERSI42 PAGE ON GITHUB 🚀 🚀
So long, and thanks for all the fish.
The end of one cycle, the beginning of another.
For now, Reversi42 returns to rest – maybe just for a while.
Next time, it might awaken to play on a quantum computer, finding the perfect move beyond human reach.