Se Téseo (Θησεύς), eroe spregiudicato nonchè figlio del re ateniese Ègeo (Αἰγεύς), avesse conosciuto qualche rudimento di Perl, avrebbe potuto risolvere brillantemente il problema del Labirinto di Cnosso adottando l’algoritmo deep-first search, sconfiggere il Minotauro (Μινώταυρος) Asterione ma – soprattutto – non avrebbe spezzato il cuore della povera Arianna (Αριάδνη), figlia di Minosse e Pasifae (ed anche madre del Minotauro), seducendola per ottenere il risolutivo gomitolo di filo rosso (un surrogato di stack analogico ideato da Dedalo ) per poi abbandonarla ancora dormiente nell’isola deserta di Nasso (pare pure dopo una lunga notte di “festeggiamenti” nella sua nave).
A chi mi obietta – ingiustamente – che ai tempi non era disponibile un interprete Perl così come un notebook agevolmente trasportabile in un Labirinto, ma anche a tutti gli altri che gridano vendetta contro il comportamento di Téseo nei confronti della povera Arianna, consiglio vivamente la lettura dell’avvincente leggenda del Minotauro; scoprirete che la storia di Téseo, per opera di Poseidone, si conclude in modo tragico a causa dell’inversione di un’informazione booleana (1 bit) ma vitale: il colore delle vele della sua imbarcazione.
Dopo questa mitologica premessa, certo di esser perdonato per eventuali errori sulla mitologia greca, sperando di non deludere il forse unico temerario lettore che avrà avuto l’ardore di proseguire nella lettura di questo articolo, vi presento un semplicissimo generatore e risolutore di labirinti scritto interamente in Perl.
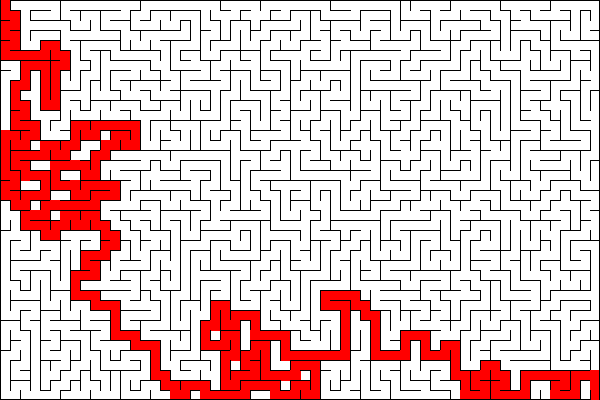
Questo progetto è ispirato da un articolo che ho letto nel blog di Eriol in cui il problema viene affrontato in Python.
In rete esistono anche molti riferimenti sui labirinti (storia, classificazione, generazione, risoluzione, miti e leggende) dove è piacevole perdersi:
- Maze Generation
- Think Labyrinth: Maze algorithms
- Maze Solving Algorithm
- Maze
- Mazework – How to build a Maze citato nell’articolo
- Labirinto
- labirinti e matematica
Nella mia implementazione, esaltando alcune caratteristiche tipiche del Perl, ho progettato delle strutture dati leggere ed efficienti (memorizzo solo le aperture del labirinto) ed ho adottato la versione dell’algoritmo depth-first search ricorsiva sia per la costruzione del labirinto (metodo Maze::asterione) che per la ricerca del percorso che conduce dall’ingresso all’uscita (metodo Maze::teseo).
Sono disponibili:
l’output del labirinto generato e risolto in modalità ASCII (Maze::toText):

l’output in formato PNG(Maze::toImage):
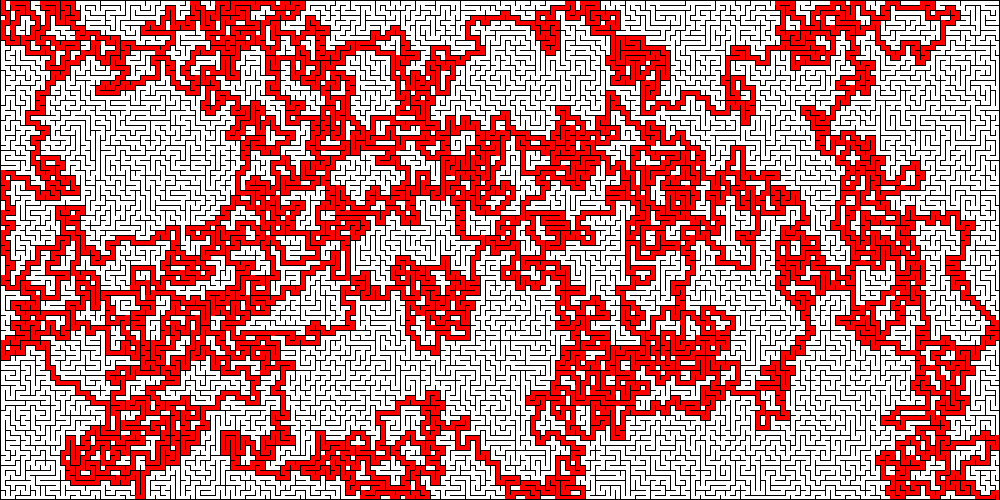
Per la generazione dell’immagine si richiedono le librerie GD.
Il tutto sarebbe ottimizzabile e migliorabile ma al momento sono già abbastanza soddisfatto dei risultati ottenuti!

Potete scaricare i sorgenti di maze.pl nel repository del progetto su github (software libero rilasciato sotto licenza GNU/GPL v. 3)
#!/usr/bin/perl
use strict;
use warnings;
package Maze;
use Carp qw(croak verbose);
use GD;
sub new {
my ($class, $x, $y) = @_;
my $self = {
x => $x,
y => $y,
doors => [],
solution => [],
};
bless $self;
$self->openWall(0, 0, 'N');
$self->openWall($x - 1, $y - 1, 'S');
return $self;
}
sub _getWallIndex($$$){
my ($self, $x, $y, $dir) = @_;
my @idx =
$dir eq 'N' ? ($x, $y, 'N') :
$dir eq 'S' ? ($x, $y + 1, 'N') :
$dir eq 'W' ? ($x, $y, 'E') :
$dir eq 'E' ? ($x + 1, $y, 'E') :
croak "wrong direction";
return @idx;
}
sub isWallOpen($$$){
my ($self, $x, $y, $dir) = @_;
my ($wx, $wy, $wdir) = $self->_getWallIndex($x, $y, $dir);
return $self->{door}[$wx][$wy]{$wdir} || 0;
}
sub openWall($$$) {
my ($self, $x, $y, $dir) = @_;
my ($wx, $wy, $wdir) = $self->_getWallIndex($x, $y, $dir);
$self->{door}[$wx][$wy]{$wdir} = 1;
}
sub getCellNeighbors($$$){
my ($self, $x, $y) = @_;
grep {
$_->[0] >= 0 and $_->[0] < $self->{x} and
$_->[1] >= 0 and $_->[1] < $self->{y}
} (
[$x - 1, $y , 'W'],
[$x + 1, $y , 'E'],
[$x , $y - 1, 'N'],
[$x , $y + 1, 'S']
);
}
sub getCellOpenedNeighbors($$$){
my ($self, $x, $y) = @_;
grep {
my (undef, undef, $dir) = @$_;
$self->isWallOpen($x, $y, $dir)
} $self->getCellNeighbors($x, $y);
}
sub isCellExit($$$){
my ($self, $x, $y) = @_;
return
($x == $self->{x} -1 ) && ($y == $self->{y} -1 );
}
sub markSolution($$$){
my ($self, $x, $y) = @_;
$self->{solution}[$x][$y] = 1;
}
sub isSolution($$$){
my ($self, $x, $y) = @_;
$self->{solution}[$x][$y];
}
# generate maze
sub asterione($$$$){
no warnings 'recursion';
my ($self, $x, $y, $visited) = @_;
$visited->[$x][$y] = 1;
return if $self->isCellExit($x,$y);
my @neighbors = $self->getCellNeighbors($x, $y);
while (scalar @neighbors){
my ($tox, $toy, $dir) =
@{ splice(@neighbors, rand(@neighbors), 1) };
next if $visited->[$tox][$toy];
$self->openWall($x, $y, $dir);
$self->asterione($tox, $toy, $visited);
}
}
# solve maze
sub teseo($$$$){
no warnings 'recursion';
my ($self, $x, $y, $visited) = @_;
$visited->[$x][$y] = 1;
if ($self->isCellExit($x, $y)){
$self->markSolution($x, $y);
return 1;
}
my @neighbors = $self->getCellOpenedNeighbors($x, $y);
while (scalar @neighbors){
my ($tox, $toy, $dir) =
@{ splice(@neighbors, rand(@neighbors), 1) };
next if $visited->[$tox][$toy];
my $isSolution = $self->teseo($tox, $toy, $visited);
if ($isSolution){
$self->markSolution($x, $y);
return 1;
}
}
return 0;
}
sub toText(){
my $self = shift;
my ($x, $y, @l1, @l2);
my $out = '';
for ($y = 0; $y < $self->{y}; $y++){
@l1 = @l2 = ();
for ($x = 0; $x < $self->{x}; $x++){
my $solution = $self->isSolution($x, $y) ? '.' : ' ';
push(@l1, $self->isWallOpen($x, $y, 'N') ? $solution x 2 : '-' x 2);
push(@l2, $self->isWallOpen($x, $y, 'W') ? ' ' : '|');
push(@l2, $solution x 2);
}
push(@l2, $self->isWallOpen($x, $y, 'E') ? ' ' : '|');
$out .=
'+' . join('+',@l1) . '+' . "\n" .
join('',@l2) . "\n";
}
@l1 = ();
for ($x = 0; $x < $self->{x}; $x++){
my $solution = $self->{solution}[$x][$self->{y} -1] ? '.' : ' ';
push(@l1,
$self->isWallOpen($x, $self->{y} -1, 'S') ?
$solution x 2 : '-' x 2
);
}
$out .= '+' . join('+', @l1) . '+' . "\n";
print $out;
}
sub toImage($$){
my ($self, $FILENAME) = @_;
my ($WX, $WY) = (10, 10);
my ($SIZEX, $SIZEY) = ($self->{x} * $WX, $self->{y} * $WY);
my $img = new GD::Image->newTrueColor($SIZEX,$SIZEY)
or croak "Can't create GD::Image";
my $cl_white = $img->colorAllocate(255,255,255);
my $cl_black = $img->colorAllocate( 0, 0, 0);
my $cl_red = $img->colorAllocate(255, 0, 0);
$img->fill( 0, 0, $cl_white);
open(my $fh, '>', $FILENAME)
or croak "Can't open $FILENAME: $!";
binmode $fh;
my ($xx, $yy);
YY: for ($yy = 0; $yy < $self->{y}; $yy++){
XX: for ($xx = 0; $xx < $self->{x}; $xx++){
$img->filledRectangle(
$xx * $WX, $yy * $WY, ($xx + 1) * $WX, ($yy + 1) * $WY,
$cl_red
)
if $self->isSolution($xx, $yy);
$img->line(
$xx * $WX, $yy * $WY, ($xx + 1) * $WX, $yy * $WY,
$cl_black
)
unless $self->isWallOpen($xx, $yy, 'N');
$img->line(
$xx * $WX, $yy * $WY, $xx * $WX, ($yy + 1) * $WY,
$cl_black
)
unless $self->isWallOpen($xx, $yy, 'W');
}
$img->line(
$xx * $WX - 1, $yy * $WY, $xx * $WX -1, ($yy + 1) * $WY,
$cl_black
)
unless $self->isWallOpen($xx - 1, $yy, 'E');
}
for ($xx = 0; $xx < $self->{x}; $xx++){
$img->line(
$xx * $WX, $yy * $WY - 1, ($xx + 1) * $WX, $yy * $WY - 1,
$cl_black
)
unless $self->isWallOpen($xx, $yy - 1, 'S');
}
print $fh $img->png(0);
close $fh;
}
package main;
# init
my $m = Maze->new(60,40);
# generate paths
$m->asterione(0,0,[]);
# solve maze
$m->teseo(0,0,[]);
# generate PNG
$m->toImage('out.png');
# print ASCII
#$m->toText();