
La rappresentazione dell’insieme di Mandelbrot, considerato uno dei frattali più popolari, è tra i miei algoritmi di prova preferiti quando studio un nuovo linguaggio di programmazione.
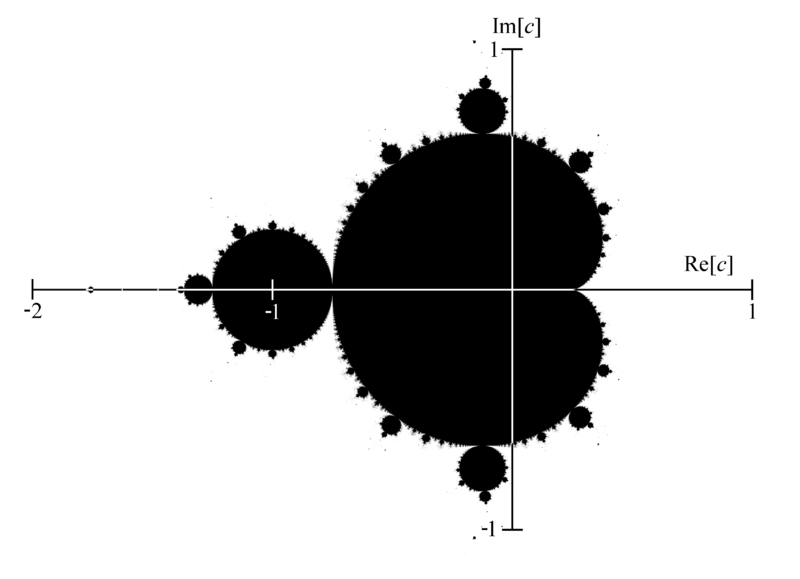
L’algoritmo di base è estremamente semplice e si presta facilmente ad esser parallelizzato.
Recentemente, all’interno dei Google Labs, è stata rilasciata un’applicazione Web che, sfruttando le API di Google Maps e canvas di HTML5, permette la navigazione all’interno dell’insieme di Mandelbrot o di altri frattali (es. Julia); vi consiglio di utilizzarla per un tour veloce.
Definizione formale
L’insieme di Mandelbrot è definito come il sottoinsime del piano complesso per cui la successione ricorsiva:
al tendere di n all’infinito, rimane limitata nel suo modulo, ovvero:
Sorgente perl
Ecco un sorgente perl che rappresenta l’insieme in modalità rigorosamente monocromatica:
#!/usr/bin/perl
##########################
# M A N D E L B R O T
# Luca Amore
##########################
use strict;
use warnings;
use GD;
my $FILENAME = 'mandelbrot.png';
my $ITERATIONS = 30;
my ($SIZEX, $SIZEY) = (700, 400);
my ($RE_MIN, $RE_MAX) = (-2.5, 1.0);
my ($IM_MIN, $IM_MAX) = (-1.0, 1.0);
my $re_factor = ($RE_MAX - $RE_MIN) / $SIZEX;
my $im_factor = ($IM_MAX - $IM_MIN) / $SIZEY;
my $img = new GD::Image->newTrueColor($SIZEX,$SIZEY)
or die "Can't create GD::Image";
# palette
my $cl_black = $img->colorAllocate( 0, 0, 0);
my $cl_white = $img->colorAllocate(255,255,255);
open(my $fh, '>', $FILENAME)
or die "Can't open $FILENAME: $!";
binmode $fh;
my $C_im = $IM_MIN;
YY: for (my $yy=0; $yy < $SIZEY; $yy++){
my $C_re = $RE_MIN;
XX: for (my $xx=0; $xx < $SIZEX; $xx++){
my ($Z_re, $Z_im, $i) = (0,0);
# Z0=0, Zn+1 = Zn^2 + C
ESCAPE_ITERATIONS: for ($i = 1; $i < $ITERATIONS; $i++){
my ($Z_re2, $Z_im2) = ($Z_re * $Z_re, $Z_im * $Z_im);
last ESCAPE_ITERATIONS unless ($Z_re2 + $Z_im2 < 4);
# (a+bi)^2 = a^2 + 2abi - b^2
$Z_im = 2 * $Z_re * $Z_im + $C_im;
$Z_re = $Z_re2 - $Z_im2 + $C_re;
} # end: ESCAPE_ITERATIONS
# draw pixel
$img->setPixel(
$xx, $yy, $i == $ITERATIONS ? $cl_black : $cl_white
);
$C_re += $re_factor;
} # end: XX
$C_im += $im_factor;
} # end: YY
# save image
print $fh $img->png(0);
close $fh;
Il codice è stato mantenuto semplice per facilitare le modifiche e la comprensione.
E’ richiesto il package GD per la produzione dell’immagine di output in formato PNG: “mandelbrot.png“.
Colori
Normalmente, per rendere tale frattale più gradevole, nella sua rappresentazione più semplice, si colorano i punti esterni all’insieme in funzione della velocità con la quale divergono a più infinito. Per la colorazione dei punti interni ed esterni esistono una miriade di algoritmi di complessità crescente; alcuni spunti interessanti.
Insieme di Julia
Una variante dell’insieme di Mandelbrot è l’insieme di Julia definito in questo modo:
Rispetto all’insieme di Mandelbrot cambia la successione ricorsiva ed è stata introdotta una costante complessa K.
Analogamente a Mandelbrot i punti appartenenti all’insieme di Julia sono quelli per cui il modulo della successione ricorsiva non diverge.
Alcuni valori di K che si consiglia di esplorare:
- K = 0.353+0.288i
- K = -0.70176-0.3842i
- K = -0.835-0.2321i
- K= -0.45+0.1428i
Dopo aver adeguato lo script perl, ho rappresentato questi insiemi di Julia:
Riferimenti
Mandelbrot Set – Wikipedia
Mu-Ency – The Encyclopedia of the Mandelbrot Set
The Mandelbrot Set (algoritmo tracciamento)
Julia Set – Wikipedia
Esplorazione
Visual Guide To Patterns In The Mandelbrot SetMandelbrot: World Map and Popular Tourist Areas




Pingback: Frattanto nella blogosfera « Ok, panico
Pingback: Erlang e frattali: fuga verso l’infinito… | Amori in corso
12-minute Mandelbrot: fractals on a 50 year old IBM 1401 mainframe
http://www.righto.com/2015/03/12-minute-mandelbrot-fractals-on-50.html