Nei giochi di strategia a turni, ho sempre ammirato le grandi sfide tra uomo e calcolatore; epiche battaglie tra pensiero strategico umano e forza tattica del calcolatore; equilibrio precario tra sinapsi e silicio, agilità contro forza, tensione tra grande visione d’insieme ed imponente valutazione di ogni dettaglio. L’epilogo può essere violento: il pensiero strategico umano si prende gioco della miopia del calcolatore e lo annichilisce; la forza bruta del calcolatore devasta il giocatore umano conducendolo verso una combinazione di cui ha previsto ogni minima variante.
Sfide dove a vincere è sempre l’uomo: il grande maestro oppure la squadra di progettisti che ha concepito un giocatore artificiale in grado di competere contro la finezza del pensiero umano.
In questo articolo, ho trovato una citazione degli autori del programma scacchistico Deep Throught (precursore di Deep Blue) sullo stile di gioco del calcolatore:
“… il computer non imita il pensiero umano – raggiunge gli stessi obiettivi per vie diverse. Vede lontano, ma osserva poco; ricorda tutto, ma non impara niente. Non fa sbagli clamorosi, ma non si innalza mai al disopra della sua normale abilità. Eppure talvolta produce intuizioni che sfuggono anche a grandi maestri.”
(Hsu, F., Anantharaman, T., Campbell, M., Nowatzyk, A. – “A Grandmaster Chess Machine“, Scientific American, Ottobre 1990)
realizzazione di Reversi42 in Python
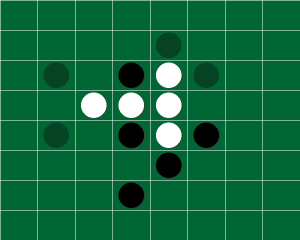
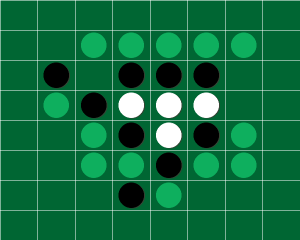
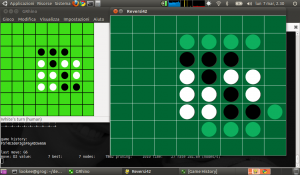
In questi giorni ho provato a realizzare un prototipo di giocatore automatico di Reversi in Python (sto approfondendo ancora la conoscenza di questo linguaggio) che ho battezzato Reversi42 (in onore di Douglas Adams e della famosa domanda: “The Ultimate Question of Life, the Universe and Everything“).
Non finirò mai di ringraziare Donato Barnaba, maestro della FNGO (Federazione Nazionale Gioco Othello), per il suo prezioso aiuto, la sua disponibilità e grande competenza (anche dal punto di vista dei giocatori automatici); senza di lui lo sviluppo di Reversi42 non sarebbe stato così stimolante e divertente! Reversi42, allo stato attuale, è solo un prototipo; eventuali imprecisioni sono da attribuire solo a me!
Reversi42, come altre mie realizzazioni, è un software libero rilasciato sotto la licenza GNU/GPL; siete incoraggiati a studiarne il sorgente, migliorarlo e farci tutto ciò che desiderate; ogni commento o contributo sarà gradito.
Di Reversi esiste un libro di Brian Rose che lo presenta così: “un minuto per imparare… una vita per diventare maestri”; le regole del gioco sono facili da apprendere (e quindi da codificare) ma il gioco può essere estremamente complesso dal punto di vista strategico e tattico (ottima sfida per la realizzazione di un giocatore automatico).
Nella progettazione del motore AI di gioco, ho deciso di adottare l’approccio classico che viene adottato in tutti i giochi di strategia ad informazione perfetta per due giocatori: si esplora in profondità l’albero delle possibili mosse valutando la bontà di ogni posizione ottenuta; si assume, inoltre, che l’avversario risponda sempre con la migliore mossa disponibile.
Trattandosi di un prototipo, sviluppato principalmente nei ritagli di tempo, ho voluto concentrare la mia attenzione solo sugli algoritmi e non sull’ottimizzazione delle singole procedure.
Citando Donald E. Knuth:
“We should forget about small efficiencies, say about 97% of the time: premature optimization is the root of all evil. Yet we should not pass up our opportunities in that critical 3%. A good programmer will not be lulled into complacency by such reasoning, he will be wise to look carefully at the critical code; but only after that code has been identified”.
Ho comunque introdotto alcune metriche (certamente migliorabili) per valutare efficienza e sensitività (rispetto a modifiche) dei punti critici dell’algoritmo.
La guida di riferimento che ho adottato è: “Stategy Game Programming” di Martin Fierz che propone un graduale ed avvincente percorso tra le principali tecniche adottate per la costruzione di un buon giocatore automatico per giochi strategici (es. scacchi, dama, Reversi, forza quattro).
Le problematiche affrontate nella realizzazione del prototipo sono:
- ricerca nell’albero delle posizioni della mossa più efficace
- realizzazione di una buona valutazione della posizione
- sintesi delle regole del gioco Reversi
Ricerca nell’albero delle posizioni della mossa più efficace
Lo scopo di questo problema (indipendente dal tipo di gioco) è quello di costruire l’albero di tutte le mosse possibili e percorrerlo in profondità ricercando la mossa migliore; si assume che l’avversario giochi sempre le mosse migliori.
All’aumentare della profondità di analisi (D), che condiziona la forza del giocatore, il numero di mosse da valutare (M) cresce esponenzialmente in funzione del fattore Branch Factor medio (B) tipico di ogni gioco.
Valori tipici del Branch Factor medio (B):
| Gioco | Branch Factor (B) |
|---|---|
| Reversi | 7 |
| Forza quattro | 7 |
| Dama | 10 |
| Scacchi | 40 |
| Go | 300 (!!!) |
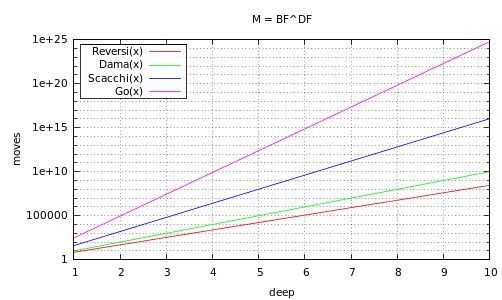
andamento del numero di mosse da analizzare al variare del gioco e profondità (in scala semilogaritmica)
Il mio obiettivo era quello di raggiungere una profondità di gioco (D) di 5-8 al fine di realizzare un giocatore automatico discreto; sul mio netbook riesco a giocare, a profondità (D) pari a 6, con tempi di attesa sempre ragionevoli (inferiori al minuto).
L’algoritmo di ricerca adottato è quello della potatura alfa-beta (in forma negamax), estremamente più efficace del minimax poichè è in grado di escludere dalla ricerca (pruning) interi rami dell’albero che condurrebbero a mosse non convenienti rispetto ad altre già individuate.
Per massimizzare il numero di rami da potare è opportuno introdurre un criterio euristico per ordinare in sequenza le mosse da valutare; le migliori mosse dovrebbero esser analizzate per prime. Rispetto all’algoritmo minimax, che richiede l’analisi di tutto l’albero delle possibili mosse (), nel caso migliore della potatura alfa beta, ovvero nel caso ideale di ordinamento perfetto (le mosse più forti vengono valutate per prime), le posizioni da analizzare si abbattono a
; siamo in grado di raddoppiare la profondità di analisi a parità di risorse di calcolo impiegate!
Il criterio euristico, con il quale vengono ordinate le mosse prima dell’alfa-beta su Reversi42, è quello di assegnare una priorità statica a tutte le mosse della scacchiera; le celle che hanno un valore più basso hanno maggiore priorità e vengono esplorate per prime (es. gli angoli).
| 1 | 8 | 7 | 6 | 6 | 7 | 8 | 1 |
| 8 | 9 | 7 | 4 | 4 | 7 | 9 | 8 |
| 7 | 5 | 3 | 2 | 2 | 3 | 5 | 7 |
| 6 | 4 | 2 | 2 | 4 | 6 | ||
| 6 | 4 | 2 | 2 | 4 | 6 | ||
| 7 | 5 | 3 | 2 | 2 | 3 | 5 | 7 |
| 8 | 9 | 7 | 4 | 4 | 7 | 9 | 8 |
| 1 | 8 | 7 | 6 | 6 | 7 | 8 | 1 |
Da quando è stato adottato questo ordinamento, le prestazioni della ricerca sono aumentate notevolmente; molto spesso la mossa migliore ricade tra le prime analizzate.
Valutazione della posizione
La valutazione della posizione è un elemento cruciale di un giocatore artificiale in quanto ne condiziona: strategia, tattica ed efficienza. Occorre ponderare due parametri contrastanti: l’accuratezza dell’analisi e l’efficienza computazionale. Riuscire a trovare un compromesso ottimale tra queste due caratteristiche è un arte che si affina con l’esperienza! Un algoritmo di valutazione troppo accurato potrebbe rallentare la ricerca e quindi penalizzare eccessivamente la profondità di analisi; un algoritmo rapido ma poco accurato potrebbe perdere grandi opportunità.
In questo prototipo ho impostato la partita su due momenti distinti:
- apertura e mediogioco: meno del 70% delle pedine non sono state giocate
- finale: almeno il 70% delle pedine sono state giocate
In apertura e mediogioco ho cercato di massimizzare la mobilità, ovvero il numero di mosse disponibili che potranno essere utilizzate per dominare il finale; ho anche assegnato dei pesi ad alcune case strategiche che concorrono alla conquista degli angoli (caselle stabili).
| 10 | -3 | 0 | 0 | 0 | 0 | -3 | 10 |
| -3 | -7 | 0 | 0 | 0 | 0 | -7 | -3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| -3 | -7 | 0 | 0 | 0 | 0 | -7 | -3 |
| 10 | -3 | 0 | 0 | 0 | 0 | -3 | 10 |
Vengono assegnati punti di bonus se si occupano angoli mentre, se si conquistano delle case adiacenti agli angoli, vengono assegnate delle penalità poiché sarà più difficile difendere l’angolo dalla conquista avversaria. Le case adiacenti all’angolo perdono la loro penalità quando l’angolo è conquistato.
Nel finale si ricerca la vincita della partita oppure, grazie alla mobilità ottenuta in apertura e nel mediogioco, si inizia a massimizzare il numero di pedine possedute rispetto a quelle dell’avversario. L’errore fatale, tipico di giocatori mediocri di Reversi, è proprio quello di perseguire intuitivamente tale obiettivo sin dalla prima mossa.
Sorgenti
Visualizza o scarica i sorgenti dal repository su github
richiede:
python-pygame – SLD bindings for games development in Python