Uno dei post che ha generato il maggior interesse in questo blog è certamente quello dedicato alla face detection tramite OpenCV. Riprendiamo questo tema dopo molto tempo parlando degli algoritmi alla frontiera per il Face Detection e Face Recognition. Lo scopo del post è fare il punto sullo stato dell’arte ed indirizzare verso mouduli open source liberamente e facilmente utilizzabili nelle applicazioni reali.

La Face Detection è l’elaborazione che ha lo scopo di rilevare la presenza di volti umani all’interno di un’immagine digitale; nel precedente articolo è stata affrontata solo questa tematica attraverso algoritmi tradizionali ma consolidati.
Gli algoritmi di Face Detection si sono evoluti nel tempo migliorando l’accuratezza della rilevazione anche attraverso l’uso di reti neurali convoluzionarie (CNN) o reti Deep Learning opportunamente strutturate ed addestrate; tale processamento sfrutta massivamente l’eventuale presenza di moderne GPU o NPU per aumentarne l’efficienza ed il parallelismo. Nel nostro caso specifico ci siamo limitati al riconoscimento di volti umani in posizione frontale.

Il benchmark estremo che ho utilizzato per mettere alla prova i moduli python individuati, è un breve video tratto dal dialogo tra Neo e l’Architetto in Matrix Reloaded; nel video, in un’atmosfera surreale, sono presenti innumerevoli volti che variano rapidamente per dimensione, inclinazione, espressione, presenza o meno di occhiali. Un video estremo di prova che farà friggere neuroni e sinapsi anche alle più evolute e performanti reti neurali convoluzionarie.
Questo è il video che è stato prodotto attraverso la nostra elaborazione:
Il modulo Python che, almeno nei miei esperimenti, ha dimostrato i migliori risultati in termini di qualità e prestazioni è MTCNN; in esecuzione su una sessione Colab con GPU attiva elabora efficientemente il flusso di frame con un livello di accuratezza molto alto se si escludono i volti in posizione non frontale. Nel video prodotto si trova l’esito dell’elaborazione dove, oltre ai volti, sono stati marcati anche alcuni punti caratteristici del viso (occhi, naso, estremi della bocca). Questo modulo è quello che riesce a rilevare meglio volti di dimensioni più piccole e non perfettamente allineati garantendo anche un’efficienza molto più alta degli altri moduli provati; MTCNN fornisce, per ogni volto rilevato, anche un livello di confidenza nella rilevazione (in tutto il video ho trovato solo un falso positivo pertanto non ho ritenuto necessario introdurre una soglia).
In alternativa, si propone l’uso del modulo: face_recognition che ha comunque garantito un’ottima precisione su volti di dimensioni significative ed un’efficienza adeguata; su tale modulo è possibile variare l’algoritmo di rilevamento (CNN o HOG) ed effettuare del tuning per cercare di rilevare volti di dimensioni minori. Sul benchmark utilizzato la rilevazione CNN non riusciva ad intercettare gli stessi volti di MTCNN mentre la rilevazione HOG, oltre a non velocizzare molto il processamento, riduceva drasticamente il numero di volti rilevati. In condizioni normali anche questo modulo è da considerare un’ottima scelta e noi lo useremo per effettuare anche il Face Recognition. Questo modulo può richiedere un quantitativo di memoria sulla GPU più elevato soprattutto se si vogliono rilevare i volti con dimensioni più piccole.

Dopo aver rilevato ed isolato i volti, l’elaborazione della Face Recognition ci permette l’associazione di un volto ad una persona. In assenza di informazioni o di preappendimento sulle persone da ricercare, è possibile aggregare i volti su possibili individui basandosi sulla similitudine delle caratteristiche fisiologiche e biometriche. Gli algoritmi per effettuare tale riconoscimento, per codificare un volto in un insieme di parametri comparabili sono davvero molteplici e tutti estremamente interessanti. Anche in questo caso le reti neurali convoluzionarie (CNN) offrono un contributo importante a questi algoritmi.

Per implementare un Face Recognition in pochissime righe di codice Python ed in modo efficiente è possibile usare il modulo face_recognition; se si vuole approfondire come questo modulo funziona internamente vi consiglio di leggere questo aricolo.

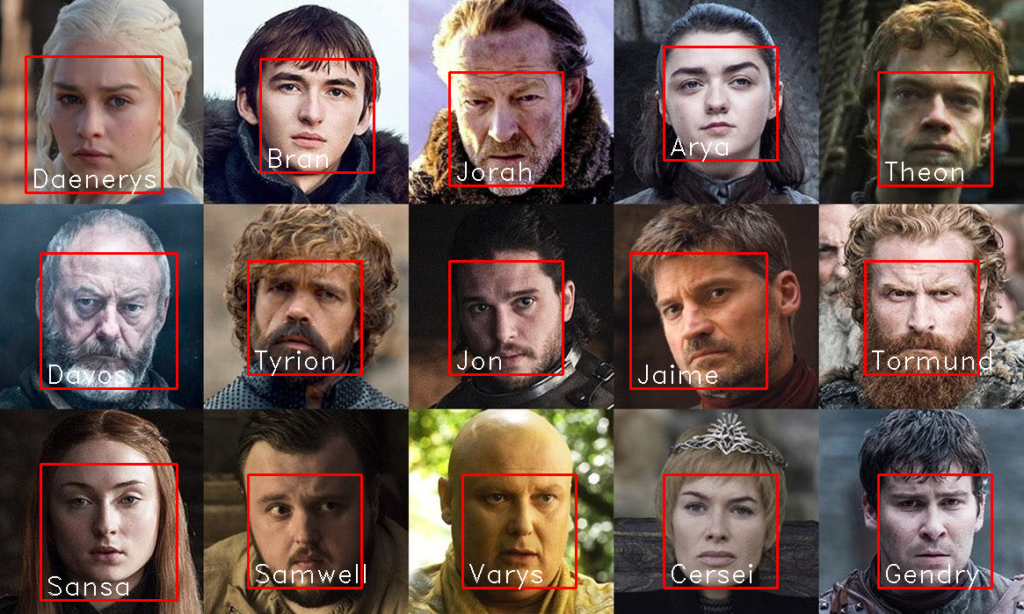
In questo caso ho creato un notepad colab di test che da una foto iniziale acquisisce le caratteristiche fisiologiche e biometriche dei vari personaggi della serie Il Trono di Spade; il modulo utilizzato, alla versione attuale, dovrebbe rappresentare ciascun volto tramite 128 parametri caratteristici.

Per testare il rilevamento ho provato a far riconoscere i personaggi su altre foto contenenti anche personaggi non presenti all’interno della foto di apprendimento; i risultati sono impeccabili. Il modulo utilizzato ha un’accuratezza eccellente sia per quanto riguarda i personaggi appresi che per quelli non analizzati che non ha mai classificato come falsi positivi.

Per spingere oltre il test abbiamo avviato la detection su foto in cui gli attori non appaiono con i costumi di scena ed hanno acconciature o il colore dei capelli totalmente differente dai personaggi che hanno interpretato; anche in questo caso l’algoritmo non sbaglia e non rileva mai falsi positivi.
Anche se non ho effettuato delle prove dirette, sono convinto che l’algoritmo scali bene all’aumentare del numero delle persone da rilevare; non ho provato a sottoporre qualche foto degli attori quando erano più giovani.
NOTEBOOK COLAB – UTILIZZATO PER LA FACE DETECTION E FACE RECOGNITION
Concludiamo dicendo che oltre alla Face Detection ed alla Face Recognition ai volti possono essere applicati altri algoritmi per l’estrazione di caratteristiche molto importanti come la rilevazione del sesso, dell’età, del sentimento (es. rabbia, gioia, paura, sorpresa, …).
Fatemi sapere i vostri pareri e le vostre esperienze su Face Detection, Face Recognition nei commenti.